„Das Ergebnis der Studie ist statistisch signifikant.“ So oder so ähnlich hast du bestimmt schon mal jemanden über eine wissenschaftliche Arbeit berichten oder reden hören. Aber was ist überhaupt statistische Signifikanz?
Wie wird sie berechnet und in welchen Fällen ist dieser Begriff hilfreich?
In diesem Video bekommst du die Antworten auf all diese Fragen. Doch nicht nur das – ich erkläre dir auch, warum statistische Signifikanzen trügerisch sein können. So kannst du in Zukunft wissenschaftliche Studien und die Berichterstattung dazu kritisch betrachten und einschätzen ob hier sauber argumentiert wird.
Inhaltsverzeichnis
Statistische Signifikanz
Zu allererst müssen wir uns klarmachen, das die alltagssprachliche Bedeutung des Begriffs „Signifikanz“ eine andere als die der „statistischen Signifikanz“ ist. Wenn etwas als signifikant bezeichnet wird, dann ist es groß oder bemerkenswert. Ist etwas statistisch signifikant, heißt das aber nicht das es bedeutsam sein muss. Im Gegenteil, etwas statistisch Signifikantes kann auch sehr klein und unbedeutend sein.
Der Begriff der statistischen Signifikanz kommt zum Tragen, wenn mittels statistischer Verfahren quantitative Datensätze ausgewertet werden. Insbesondere dann, wenn das Ziel einer Studie darin besteht, den Zusammenhang zweier Variablen auf mögliche Effekte hin zu überprüfen.
Wird beispielsweise in einem Experiment eine unabhängige Variable manipuliert (z.B. das Verabreichen eines Nahrungsergänzungsmittels), wird der Effekt dessen auf die abhängige Variable gemessen (z.B. die Kraftausdauer im Training). Ist dieser Effekt statistisch signifikant, sind alle happy und wir können nach Hause gehen.
Nein, so einfach ist es natürlich nicht. Aber dazu kommen wir später.
Die statistische Signifikanz dient zur Überprüfung, wie wahrscheinlich das Ergebnis einer Messung nur durch Zufall entstanden ist, oder ob tatsächlich ein Effekt besteht.
Kommen wir zu dem Schluss, dass ein Ergebnis statistisch signifikant ist, dann besteht Grund zur Annahme, dass das Ergebnis der Analyse einer ausgewählten Stichprobe auch für die Grundgesamtheit gilt.

Statistische Signifikanz und die Stichprobengröße
In der Regel werden Studien ja nicht mit allen möglichen Menschen, die eine bestimmte Gruppen repräsentieren (die Grundgesamtheit) durchgeführt, sondern mit einer Stichprobe dieser Grundgesamtheit.
Führst du beispielsweise eine Umfrage durch, dann nehmen vielleicht 200 Personen daran teil. Bei einem Experiment sind es vielleicht 60. Oder aber du hast Daten aus sozialen Medien oder von Unternehmen gesammelt, in denen die 1000 oder noch mehr Datensubjekte zu finden sind.
Die Größe all dieser Stichproben ist bei der Interpretation von Signifikanztests zu beachten. Je kleiner die Stichprobe ist, desto schwieriger wird es, einen statistisch signifikanten Zusammenhang zu entdecken. Das liegt daran, dass der Zufall immer mehr Einfluss gewinnt und ein sehr großer Effekt vorliegen muss, damit der Zufall statistisch ausgeschlossen werden kann.
Je größer die Stichprobe, desto schneller lassen sich statistisch signifikante Zusammenhänge messen. Das liegt daran, dass sich große Stichproben immer mehr der Grundgesamtheit annähern und ein zufälliges Ergebnis immer unwahrscheinlicher wird.
p-Wert, Teststatistik und Nullhypothese
Eine mathematische Größe, die für einen Test der statistischen Signifikanz von Bedeutung ist, ist der p-Wert. Der p-Wert fasst das Ergebnis einer Messung zusammen hilft dabei zu bestimmen, wie wahrscheinlich das Ergebnis ein zufälliges Ergebnis oder ein tatsächlicher Effekt ist. Wie groß dieser Effekt ist, lässt sich am p-Wert nicht ablesen.
Genauer gesagt, ist der p-Wert die Wahrscheinlichkeit, dass unter der Annahme, die Nullhypothese sei wahr, die Teststatistik den beobachteten oder einen extremeren Wert annimmt.
Wowowo – Moment mal – ganz langsam. Hier sind nun zwei neue Begriffe gefallen.
Teststatistik und Nullhypothese
Bei einem Sigifikanztest sind zwei Hypothesen von Bedeutung:
H0: Es besteht kein Effekt
H: Es besteht ein Effekt.
Mithilfe eines Sigifikanztests kann die Nullhypothese (H0) verworfen werden. Also zum Beispiel wenn der p-Wert unter 0.05 liegt. Wenn das der Fall ist, dann besteht Grund zur Annahme, dass ein Effekt besteht der über den Zufall hinausgeht.
Durch die Teststatistik, eine Hilfsfunktion der möglichen Ergebnisse, ergibt sich ein Ablehnungsbereich. Fällt das Ergebnis in diesen Bereich, ist die Nullhypothese abzulehnen.
Wie groß dieser Bereich ist, legt das sogenannte Sigifikanzniveau fest. Das liegt in der Regel bei 0.05, also 5%. Das hat keinen besonderen Grund, außer dass irgendjemand das mal so festgelegt hat (Dieser Jemand hieß Roland Fisher). Manchmal wird das Signifikanzniveau aber auch bei 0.01, also 1% angelegt.
Ob ein Ergebnis statistisch signifikant ist, liegt also zu einem großen Teil daran, welches Signifikanzniveau zugrunde gelegt wird. Grundsätzlich wird aber natürlich ein p-Wert umso beeindruckender, je kleiner er ist.
Hol‘ dir jetzt die Komplettlösung zum Verfassen einer herausragenden Hausarbeit:
Statistische Signifikanz mit dem Student’s t-Test bestimmen
Ein beliebter Test zur Signifikanzprüfung ist der sogenannte Student’s t-Test. Der heißt nicht so, weil er Studierende zur Verzweiflung bringen soll. Sein Erfinder William Sealy Gosset publizierte seine Gedanken zu diesem Test zunächst unter dem Pseudonym „Student“.
Der t-Test ist ein Hypothesentest und wird gerne bei kleinen Stichproben verwendet. Er hilft also dabei zu entscheiden, ob die Nullhypothese abzulehnen ist oder nicht. Die Nullhypothese wird dabei durch die t-Verteilung dargestellt, was bei kleinen Stichproben gegenüber anderen Hilfsfunktionen wie der Normalverteilung einen Vorteil bringt.
Der t-Test wird angewendet, um statistisch signifikante Unterschiede zwischen zwei Variablen festzustellen. Hier kann der Test den Mittelwert der einen Variable, mit dem Mittelwert der anderen Variable vergleichen. Das ist auch die häufigste Anwendung des Tests.
Beispiel:
Wir machen ein Experiment mit zwei Gruppen von Studierenden. Beide Gruppen schreiben die gleiche Englisch-Klausur. Eine Gruppe hat jedoch mit einer Kartei-Karten App gelernt und die andere Gruppe nicht. Wir könnten nun vermuten, dass die Gruppe mit der App bessere Ergebnisse erzielt. In einem t-Test vergleichen wir dann die Mittelwerte der Testergebnisse beider Gruppen miteinander.
Es ist aber ebenso möglich, den Mittelwert einer Variable mit einem eigenen Sollwert oder auch Erwartungswert zu vergleichen.
Die t-Verteilung folgt ebenfalls der Form einer Glocke und sieht so aus:
Für den Test wird nun ein t-Wert berechnet. Die Formel für den t-Test mit einem Mittelwert und einem Sollwert sieht so aus:
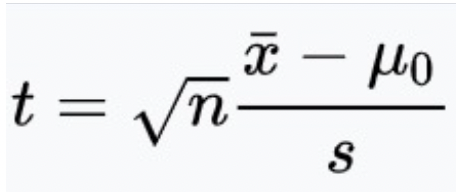
- n ist die Größe der Stichprobe
- das x mit dem Strich ist der Mittelwert in Form des arithmetischen Mittels
- das µ ist der Sollwert
- s ist die Standardabweichung der Stichprobe
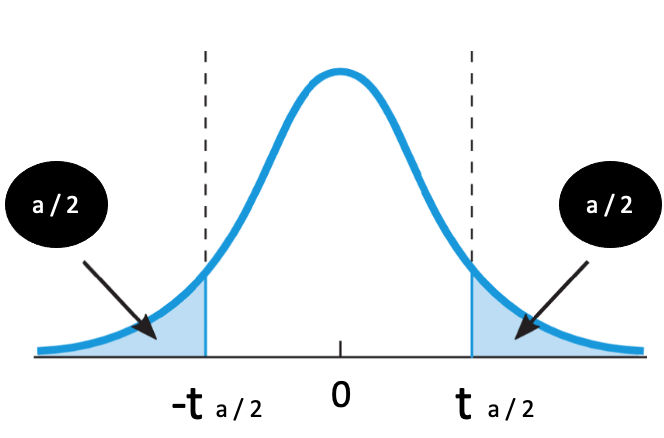
Der berechnete t-Wert wird nun ins Verhältnis zur Null gesetzt. Liegt der Wert nah bei Null, stellen wir keinen signifikanten Unterschied zwischen den Mittelwerten oder dem Mittelwert oder dem Sollwert fest. Liegt der Wert im markierten Bereich an der Peripherie der Kurve, dann weichen die Werte so stark voneinander ab, dass die Nullhypothese abzulehnen ist. Wir können also einen Effekt vermuten.
Die markierten Randbereiche (α/2) werden durch das Signifikanzniveau festgelegt. Bei einem beidseitigen Test hat man dann links 2,5% und rechts 2,5% (bei einem Signifikanzniveau von 5%). Ein beidseitiger Test wird durchgeführt, wenn die zugrundeliegende Hypothese ungerichtet ist („Es besteht (irgend-)ein Effekt“). Der Test ist einseitig, wenn unsere Vermutung gerichtet ist („Es besteht ein positiver/negativer Effekt“). Dann würde man nicht α/2, sondern nur α (also 5%) anlegen, auf der entsprechenden Seite.
Wenn du auf dem Weg zu mehr Erfolg im Studium noch ein wenig Starthilfe für deine wissenschaftliche Arbeit benötigst, dann habe noch ein PDF für dich, das du dir gratis herunterladen kannst:
Die 30 besten Formulierungen für eine aufsehenerregende Einleitung

Ein Gedanke zu „Statistische Signifikanz (einfach erklärt)“