Die Normalverteilung deiner quantitativen Daten zu überprüfen ist eine wichtige Voraussetzung für viele statistische Test. Aber was versteht man unter Normalverteilung in der Statistik und wie kannst du sie überprüfen?

In diesem Artikel lernst du 3 Dinge:

• Was ist eine Normalverteilung in der Statistik und warum ist sie wichtig?
• Welche Abweichungen gibt es und wie erkennst du sie?
• Wie testest du die Normalverteilung eines Datensatzes rechnerisch und grafisch?

Wenn du also deine eigenen Daten für eine Studie vorliegen hast und diese auf Normalverteilung prüfen musst, dann weißt du am Ende des Artikels genau was du tun musst und warum du es tust.

Was ist eine Normalverteilung in der Statistik?

Die Überprüfung der Normalverteilung ist oft der erste Schritt einer statistischen Auswertung. Die Grundlage dafür sind deine Daten, die du bei einer quantitativen empirischen Studie mittels sogenannter Messinstrumente wie einem Fragebogen erheben kannst.

Wenn die Erhebung abgeschlossen ist und dir die Daten vorliegen, dann kannst du zur Überprüfung der Normalverteilung ein Diagramm erstellen. Dieses Diagramm zeigt wie oft jeder Wert den du gemessen hast in deinem Datensatz auftaucht.

Histogramm

Das Diagramm was hierfür verwendet wird läuft auch unter dem Namen „Histogramm“ – das ist einfach der Name für die graphische Darstellung.

Bei dieser Darstellung der Häufigkeitsverteilung werden auf einer horizontalen Achse Balken generiert, die anzeigen, wie oft jeder Messwert in den Daten vorkommt. So kannst du beurteilen, wie die Daten verteilt sind.

Daten können ganz unterschiedlich verteilt sein. Eine Art der Verteilung ist die Normalverteilung. Hier taucht die Mehrzahl der Messwerte im Zentrum des Histogramms auf und die anderen Werte nehmen symmetrisch dazu immer weiter ab, je weiter es nach außen an die Ränder geht.

Gaußsche Glockenkurve

Die graphische Darstellung, die bei einer Normalverteilung auf dem Histogramm entsteht ähnelt einer Glocke. Der Mathematiker Carl Friedrich Gauß wurde für seine Arbeit über die Normalverteilung berühmt.

Im deutschen Sprachraum hat sich deshalb die Bezeichnung „Gaußsche Glockenkurve“ für eine Funktion die die Normalverteilung abbildet etabliert. Die Gaußsche Glockenkurve und ihr Entdecker haben es sogar bis auf den 10-Mark Schein gebracht.

Ein Beispiel für eine Normalverteilung

Ein klassisches Beispiel dafür ist die Körpergröße von Menschen. Du musst nur genügend Menschen nach ihrer Körpergröße fragen, um festzustellen, dass hier eine Normalverteilung vorliegt. Männer aus Deutschland sind im Durchschnitt 180 cm groß.

Dieser Wert wird sich in der Mitte des Histogramms wiederfinden, genauso wie die Werte 181 cm oder 179 cm. Je weiter wir uns von dieser Mitte entfernen, desto seltener werden Datenpunkte auftauchen. Es wird vielleicht noch ein paar Männer geben, die 195 cm groß sind, aber nur sehr wenige über 210 cm.

Die 180cm sind in diesem Beispiel der sogenannte Erwartungswert. Er liegt genau in der Mitte des Histogramms. Wenn sich der Erwartungswert ändert, verschiebt sich auch die imaginäre Glock auf der horizontalen Achse des Histogramms. Er ist auch gleichbedeutend mit dem Median der Daten.

Weitere Größen der mathematischen Formel der Normalverteilung sind Varianz und Standardabweichung. Wenn sich der Wert der Varianz ändert, streckt bzw. staucht sich deine Glocke.

Bei einer Normalverteilung liegen exakt 68,3 % der Daten in dem Bereich des Erwartungwerts +/-einer Standardabweichung (in unserem Beispiel also zwischen 170 cm und 190 cm.

Etwa 95,5 % der Daten liegen im Bereich Erwartungswert +/- der zweifachen Standardabweichung (das entspräche dem Bereich 160cm bis 200 cm).

Und ganze 99,7 % aller Daten liegen im Bereich Erwartungswert +/- die dreifache Standardabweichung (das entspräche dem Bereich 150cm bis 210 cm).

Abweichungen von der Normalverteilung

Es gibt im Grunde zwei Arten von Abweichungen bei Häufigkeitsverteilungen. Dann sind die Daten eben nicht normal verteilt. (Field, 2015)

Schiefe

Bei einer schiefen Verteilung ordnen sich die Balken nicht symmetrisch zum Mittelwert an, sondern sind nach rechts oder links verschoben.

Eine negative Schiefe (linksschiefe) liegt vor, wenn die Kurve links flach und rechts hoch ist.

Eine positive Schiefe (rechtsschiefe) liegt vor, wenn die Kurve rechts flach und links hoch ist.

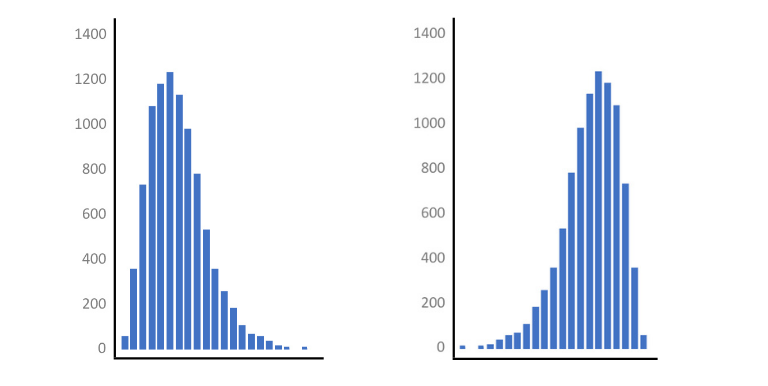
Wölbung / Kurtose

Die Wölbung hat mit dem Ausmaß der Häufigkeit von Werten an den Rändern zu tun. Wenn im Vergleich zur Normalverteilung zu wenig Werte an den Rändern liegen, dann sieht die Glocke viel zu spitz aus. Das ist dann eine positive Wölbung (positiver Exzess).

Wenn zu viele Werte an den Rändern liegen, sieht die Glocke viel zu flach aus. Das nennt man dann negative Wölbung (negativer Exzess).

Außerdem kann es vorkommen, dass sich Ausreißer ergeben und Balken ergeben, die das Bild der Glockenkurve stören.

Bei einer Normalverteilung sind Schiefe und Wölbung nicht vorhanden, also 0.

Normalverteilung prüfen

Kommen wir nun zu dem Fall, dass du deine eigenen Daten vorliegen hast und diese auf Normalverteilung testen möchtest. Das ist wichtig, da die Normalverteilung eine Voraussetzung für die Berechnung parametrischer Tests wie dem t-test, einer ANOVA oder einer Pearson-Korrelation ist.

Normalverteilung rechnerisch prüfen

Um die Normalverteilung zu testen, kannst du eines von vielen Verfahren wählen, wie beispielsweise den Shapiro-Wilk Test. Diesen kannst du mit einer Statistik-Software wie SPSS, Jamovi oder R durchführen.

Als Ergebnis bekommst du einen p-Wert. Liegt dieser unter 0,05, dann kannst du von einer statistisch signifikanten Abweichung von der Normalverteilung ausgehen. Ist der Wert größer als 0,05 dann sind deine Daten höchstwahrscheinlich normalverteilt.

Normalverteilung grafisch prüfen

Um auf Nummer Sicher zu gehen, schaust du dir aber noch das Histogramm der Häufigkeitsverteilung deiner Daten an. Das ist nötig, weil der p-Wert durch die Größe der Stichprobe beeinflußt werden kann und so nicht hundertprozentig aussagekräftig ist.

Bei der graphischen Überprüfung musst du selbst beurteilen, ob das Histogramm in etwa der Glockenkurve der Normalverteilung entspricht oder nicht.

In dieser Darstellung siehst du zwei Histogramme gegenübergestellt. Eines der beiden zeigt eine Normalverteilung und das andere eine Nicht-Normalverteilung.

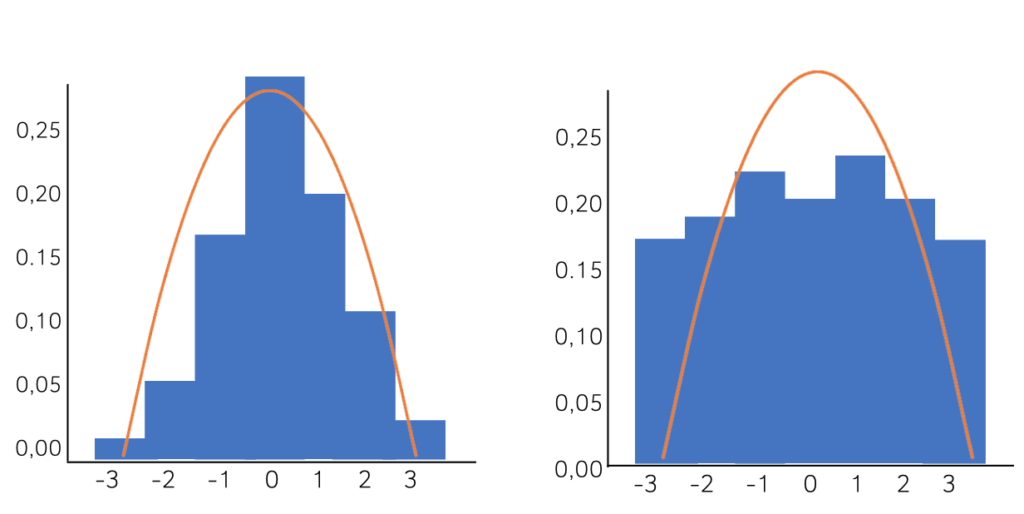
Auf der linken Seite ist die Abweichung der Häufigkeitsverteilung von der Glockenkurve sehr klein, was du mit bloßem Auge erkennen kannst.

Auf der rechten Seite siehst du eine ganz andere Darstellung im Histogramm. Hier kannst du sofort erkennen, dass keine Normalverteilung vorliegt.

Weitere Wege um die Normalverteilung zu testen sind sogenannte Boxplots oder einen QQ Plot zu erstellen und auf Symmetrie zu überprüfen.

Fazit

Der beste Weg, um auf Normalverteilung zu testen ist die Kombination aus einem statistischen Test und anschließender grafischer Überprüfung. Die statistischen Tests sind zwar hilfreich, können aber ein verzerrtes Bild darstellen.

Besonders bei mittleren oder großen Stichproben mit über 100 Beobachtungen kommt es oft vor, dass die Daten rechnerisch nicht normalverteilt sind. Eine grafische Überprüfung zeigt dann aber oft, dass sie sich im Grunde nach dem Vorbild der Glockenkurve verteilen.

Wenn du auf dem Weg zu mehr Erfolg im Studium noch ein wenig Starthilfe für deine wissenschaftliche Arbeit benötigst, dann habe noch ein PDF für dich, das du dir gratis herunterladen kannst:

Die 30 besten Formulierungen für eine aufsehenerregende Einleitung

---