Was ist eine Regressionsanalyse?

Stell dir vor, du könntest eine Vorhersage über die Zukunft treffen. Unmöglich, oder?

Nein, denn genau das ermöglicht dir eine Regressionsanalyse.

Egal ob du wissen möchtest, wie sich deine Lernstunden auf deine Noten auswirken oder wie Werbeausgaben den Umsatz beeinflussen – die Regressionsanalyse hilft dir, solche Zusammenhänge zu erkennen und in die Zukunft zu projizieren.

In diesem Artikel werde ich dir in einfachen Worten erklären, worum es sich bei der linearen und der multiplen Regression handelt.

So kannst du dein Statistikgrundwissen um einen wichtigen Baustein erweitern.

Was ist eine Regressionsanalyse?

Eine Regressionsanalyse ist ein statistisches Verfahren, mit dem die Beziehung zwischen einer abhängigen Variable (zum Beispiel der erzielten Note in einer Klausur) und einer oder mehreren unabhängigen Variablen (zum Beispiel Übungsstunden oder der Anzahl der Übungsaufgaben) untersucht wird. Das Ziel der Regressionsanalyse ist es, die Stärke und Richtung dieser Beziehungen zu bestimmen und Vorhersagen zu treffen.

Die Regressionsanalyse hilft dabei, Zusammenhänge in den Daten zu identifizieren und zu quantifizieren. Zum Beispiel könnte sie dir zeigen, wie stark die Anzahl der Übungsstunden deine Note beeinflusst und ob dieser Einfluss positiv oder negativ ist.

Durch die Erstellung eines mathematischen Modells, kannst du dann eine Vorhersage treffen, wie sich eine Änderungen in der unabhängigen Variable auf die abhängige Variable auswirken würde.

Es gibt verschiedene Arten von Regressionsanalysen, aber die drei häufigsten sind:

• Einfache lineare Regression: Diese Form der Regressionsanalyse untersucht die Beziehung zwischen einer abhängigen und einer unabhängigen Variablen. Ein weiteres Beispiel wäre eine Untersuchung dazu, wie das Marketingbudget einer Firma deren Umsatz beeinflusst.
• Multiple lineare Regression: Diese Methode ermöglicht die Analyse der Beziehung zwischen einer abhängigen Variablen und mehreren unabhängigen Variablen. Zum Beispiel könnte man untersuchen, wie Industrienähe, Abwasserzufluss und Niederschlag die Wasserqualität eines Gewässers beeinflussen
• Logistische Regression: Diese Methode wird verwendet, wenn die abhängige Variable binär ist (zum Beispiel krank/nicht krank). Sie hilft dabei, die Wahrscheinlichkeit eines bestimmten Ergebnisses vorherzusagen wie: Welche Faktoren beeinflussen die Wahrscheinlichkeit einer Herzkreislauferkrankung?

Einfache lineare Regression

Das Ziel der einfachen linearen Regression ist es, den Wert einer abhängigen Variable basierend auf einer unabhängigen Variable vorherzusagen.

Je stärker der lineare Zusammenhang zwischen den beiden Variablen ist, desto präziser wird die Vorhersage sein. Dies bedeutet, dass ein größerer Anteil der Varianz der abhängigen Variable durch die unabhängige Variable erklärt wird.

Um dies visuell darzustellen, kann man ein Streudiagramm verwenden. Wenn die Datenpunkte eng an einer Geraden liegen, zeigt dies einen starken linearen Zusammenhang.

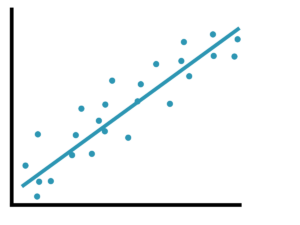
Die Grundidee der einfachen linearen Regression ist es, eine Gerade zu finden, die den bestmöglichen Fit für deine Daten darstellt. Diese Gerade wird durch die Gleichung y = a + bx beschrieben, wobei y die abhängige Variable, x die unabhängige Variable, a der Achsenabschnitt und b die Steigung der Gerade ist.

1. Daten sammeln: Zuerst brauchst du Daten. Zum Beispiel sammelst du Daten über die Übungsaufgaben und die entsprechenden Noten.
2. Daten analysieren: Nun analysierst du die Daten, um zu sehen, ob es einen Trend gibt. Das kannst du zum Beispiel mit einem Streudiagramm tun.
3. Gleichung aufstellen: Mit statistischer Software wie R, Python oder sogar Excel kannst du dann die Gleichung der Geraden berechnen. Die Software liefert dir die Werte für a und b.
4. Interpretation: Jetzt interpretierst du die Ergebnisse. Wenn b positiv ist, bedeutet das, dass mehr Übungsaufgaben zu einer höheren Anzahl an Punkten in der Klausur führen. Ist b negativ, deutet das darauf hin, dass mehr Übungsaufgaben mit schlechteren Noten korrelieren.

Praktisches Beispiel der einfachen linearen Regression

Nehmen wir an, du untersuchst, ob die Anzahl der Übungsaufgaben, die ein Student macht, seine Prüfungsergebnisse beeinflusst. Hier ist ein detailliertes Beispiel, wie du vorgehst:

1. Daten sammeln: Du hast eine Tabelle mit zwei Spalten: Anzahl der Übungsaufgaben und Punkten in der Klausur. Zum Beispiel:
   • Student A: 10 Aufgaben, Punkte: 27
   • Student B: 5 Aufgaben, Punkte: 16
   • Student C: 8 Aufgaben, Punkt: 19
   • Student D: 9 Aufgaben, Punkte: 17
   • Student E: 2 Aufgaben, Punkte: 9
2. Daten analysieren: Du erstellst ein Streudiagramm, in dem die Anzahl der Übungsaufgaben auf der x-Achse und die Noten auf der y-Achse dargestellt sind. Du erkennst einen positiven Trend, das heißt, je mehr Aufgaben gemacht wurden, desto besser die Note.
3. Gleichung aufstellen: Du nutzt Excel, um die lineare Regression durchzuführen. Die Software liefert dir die Regressionsgleichung: y= 5,75+1,74x wobei y die Anzahl der Punkte und x die Anzahl der Übungsaufgaben ist.
4. Interpretation: Der Achsenabschnitt a = 5,75 bedeutet, dass man 5,75 Klausurpunkte erzielen würde, wenn man keine Übungsaufgab macht. Die Steigung b = 1,74 bedeutet, dass jede zusätzliche Übungsaufgabe die Anzahl der Punkte um 1,74 verbessert.

Multiple lineare Regression

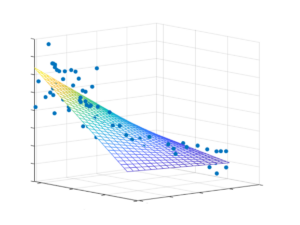
Im Gegensatz zur einfachen linearen Regression, ermöglicht die multiple lineare Regression die Berücksichtigung mehrerer unabhängiger Variablen. Das Ziel ist es, eine abhängige Variable basierend auf mehreren unabhängigen Variablen vorherzusagen. Die abhängige Variable wird oft als Kriterium bezeichnet, während die unabhängigen Variablen als Prädiktoren bekannt sind.

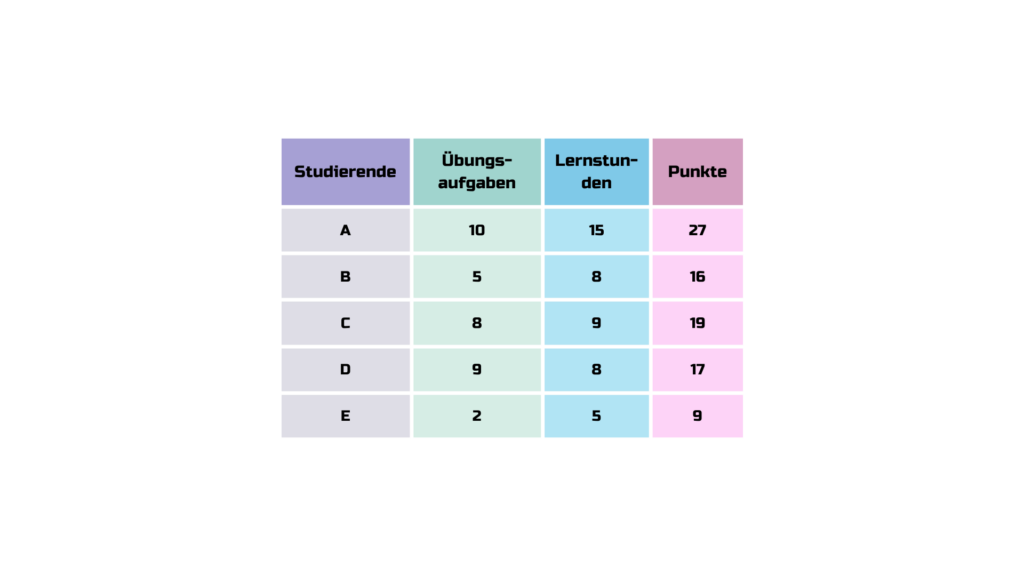
1. Daten sammeln: Die Tabelle zeigt die Anzahl der Übungsaufgaben, Lernstunden und die entsprechenden Noten der Studenten.
2. Daten analysieren: Analyse der Daten, um zu sehen, wie diese Variablen die Note beeinflussen.
3. Gleichung aufstellen: Mit Excel oder einer anderen statistischen Software erhalten wir die Regressionsgleichung: y= 0,91+0,69×1+1,31×2
   y = Anzahl Klausurpunkte
   x1= Übungsaufgaben
   x2=Lernstunden
4. Interpretation:
   • Der Achsenabschnitt a = 0,91 bedeutet, dass Anzahl der Klausurpunkte 0,91 wäre, wenn keine Übungsaufgaben oder Lernstunden erfolgt wären.
   • Die Steigung b_1 =0,69 bedeutet, dass jede zusätzliche Übungsaufgabe die Anzahl der Punkte der Klausur um 0,69 Punkte erhöht.
   • Die Steigung b_2 = 1,31 bedeutet, dass jede zusätzliche Lernstunde die Punktzahl um 1,31 erhöht.

Logistische Regression

Die logistische Regression wird verwendet, wenn die abhängige Variable nur zwei mögliche Werte hat, zum Beispiel „Bestanden“ oder „Nicht Bestanden“. Anstatt eine lineare Beziehung zu modellieren, wird mit der logistischen Regression die Wahrscheinlichkeit geschätzt, dass ein bestimmtes Ereignis eintritt. So könntest du vorhersagen, wie hoch die Wahrscheinlichkeit ist, dass ein Student, der 10 Übungsaufgaben gemacht hat, die Prüfung besteht.

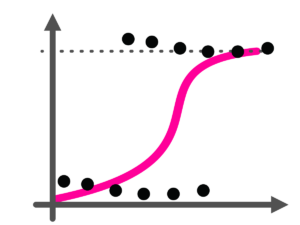
Statt einer Geraden wie bei der linearen Regression verwenden wir bei der logistischen Regression eine S-Kurve, um die Wahrscheinlichkeit darzustellen.

Daten:

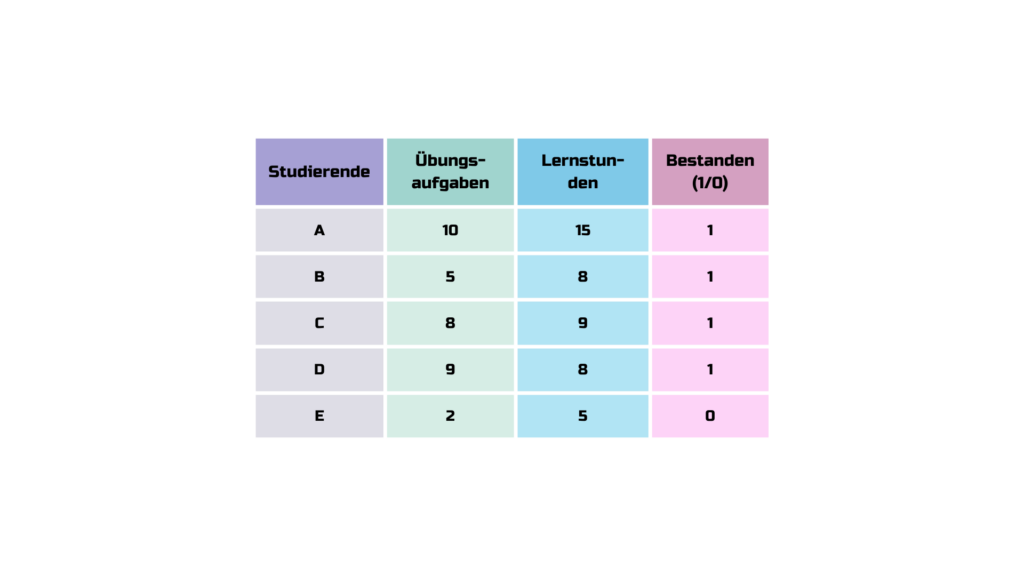
1. Daten sammeln: Die Tabelle zeigt die Anzahl der Übungsaufgaben, Lernstunden, und ob der Student die Prüfung bestanden hat (1) oder nicht (0).
2. Gleichung aufstellen: Mit einer statistischen Software erhalten wir die logistische Regressionsgleichung:
   logit(p )=−5,434+0,61×1+0,53×2 wobei P die Wahrscheinlichkeit ist, dass eine Studentin die Prüfung besteht, x_1 die Anzahl der Übungsaufgaben und x_2 die Lernstunden sind.
3. Interpretation:
   • β1 = 0,61: Jede zusätzliche Übungsaufgabe erhöht die Wahrscheinlichkeit, die Prüfung zu bestehen.
   • β2 = 0,53: Jede zusätzliche Lernstunde erhöht die Wahrscheinlichkeit, die Prüfung zu bestehen.

Skalenniveaus

	Anzahl unabhängiger Variablen	Skalenniveau abhängige Variable	Skalenniveau unabhängige Variable
Einfache lineare Regression	eine	metrisch	metrisch, ordinal, nominal
Multiple lineare Regression	mehrere	metrisch	metrisch, ordinal, nominal
Logistische Regression	mehrere	ordinal, nominal	metrisch, ordinal, nominal

Bei der Regressionsanalyse gibt es verschiedene Methoden mit spezifischen Voraussetzungen:

• Einfache und multiple lineare Regression: Beide Methoden erfordern, dass die abhängige Variable metrisch ist. Bei der einfachen linearen Regression gibt es eine unabhängige Variable, bei der multiplen linearen Regression mehrere. Die unabhängigen Variablen können metrisch, ordinal oder nominal sein.
• Logistische Regression: Diese Methode verwendet mehrere unabhängige Variablen, wobei die abhängige Variable ordinal oder nominal sein muss. Die unabhängigen Variablen können metrisch, ordinal oder nominal sein.

Diese Voraussetzungen stellen sicher, dass die Analyse valide und aussagekräftige Ergebnisse liefert.

Wenn du auf dem Weg zu mehr Erfolg im Studium noch ein wenig Starthilfe für deine wissenschaftliche Arbeit benötigst, dann habe noch ein PDF für dich, das du dir gratis herunterladen kannst:

Die 30 besten Formulierungen für eine aufsehenerregende Einleitung

---