Deskriptive Statistik – wofür brauchst du die?

Gehen wir davon aus, du hast für deine wissenschaftliche Arbeit eine Umfrage durchgeführt und 100 Personen befragt.

Jetzt hast du einen ziemlich großen Datensatz und musst irgendwie versuchen Ordnung in das Datenchaos deiner Stichprobe zu bringen.

Bevor Du deine eigentlichen Hypothesen prüfen kannst (mit Hilfe der Inferenzstatistik), brauchst du eine Vorstellung davon, wie deine Stichprobe aussieht.

Dabei hilft dir die deskriptive Statistik.

In diesem Artikel schauen wir uns deshalb die Grundlagen der deskriptiven Statistik an und klären alles was du wissen musst, um eine Stichprobe in deiner quantitativen wissenschaftlichen Arbeit zu beschreiben.

Wofür brauchst du deskriptive Statistik?

Es ist nahezu egal, in welchem Fachbereich du studierst, ein paar Grundlagen über deskriptive Statistik zu wissen ist ziemlich nützlich.

Klar, in der Uni brauchst du sie hauptsächlich dann, wenn du mit quantitativen Daten arbeitest und selbst Analysen anstellst.

Auf der anderen Seite bringt dich ein wenig Grundlagenwissen außerhalb der Uni weiter, zum Beispiel beim Interpretieren von Statistiken, die von den Medien aufbereitet werden.

Wenn du etwas Ahnung hast, kannst du ziemlich schnell erkennen, wann eine Statistik genutzt wird, um einen bestimmten Aspekt der Daten hervorzuheben und ein bestimmtes Narrativ zu unterstützen.

Also, deskriptive Statistik findet in allen Bereichen Anwendung, in denen quantitative, d.h. auf Zahlen basierende, Datensätze erhoben und ausgewertet werden.

Sie bildet die Grundlage für die Datenanalyse. Denn um deine Daten effektiv auszuwerten, ist es zunächst erforderlich, die Stichprobe zu beschreiben. Deskriptive Statistik wird daher auch als beschreibende Statistik bezeichnet.

Konkret heißt das, dass du anhand der Maßzahlen der deskriptiven Statistik beurteilen kannst, wie beispielsweise der Altersdurchschnitt deiner Umfrage aussieht. Solche demographischen Daten zu berichten, hilft nicht nur dir, sondern auch anderen deinen Datensatz besser zu verstehen.

Aber auch andere Variablen wie beispielsweise das durchschnittliche Einkommen oder die Verteilung einzelner Variablen können berücksichtigt werden.

Die deskriptive Datenanalyse bildet den Ausgangspunkt für nahezu jede statistische Analyse, weil sie festlegt, wie du weiter mit deinen Daten vorgehen solltest und welche statistischen Tests überhaupt für die Analyse Sinn machen.

Unterschied zur Inferenzstatistik

In der deskriptiven Statistik werden Stichproben beschrieben und zur besseren Übersicht in Form von Grafiken und Tabellen dargestellt.

Die induktive Statistik, auch als Inferenzstatistik bekannt, geht darüber hinaus und liefert dir Kennzahlen, mit denen du Schlussfolgerungen treffen kannst, die über eine Stichprobe hinausgehen.

Wenn beispielsweise die Einschaltquoten der Frauen Fußball-Weltmeisterschaft berechnet werden, dann nicht, indem alle 41 Millionen Haushalte in Deutschland befragt werden.

Stattdessen werden Daten über das TV-Verhalten von wenigen tausend Menschen erhoben, die repräsentativ für die deutsche Bevölkerung sind. Von dieser Stichprobe wird dann auf die Grundgesamtheit (alle TV-Zuschauer:innen in Deutschland) geschlossen.

Um solche Dinge anstellen zu können, oder wenn du in deiner wissenschaftlichen Arbeit von dir aufgestellte Hypothesen testen möchtest, dann brauchst du vor allem die Inferenzstatistik.

Kommen wir aber nun zurück zur deskriptiven Statistik.

Tabellen und Grafiken

Ein beliebtes Werkzeug der deskriptiven Statistik sind Tabellen und Grafiken.

Sie eignen sich super, um deine Daten visuell darzustellen und für deinen Ergebnisteil oder eine Präsentation aufzubereiten.

Gehen wir wieder von dem Beispiel mit den 100 Befragten aus. Der jüngste Teilnehmer deiner Studie war 20 und die älteste Teilnehmerin 50 Jahre alt. Alle anderen liegen irgendwo dazwischen. Es ist also sehr wahrscheinlich, dass du bei der Frage nach dem Alter bis zu 30 verschiedene Antworten bekommen hast.(20,21,22,23,24,25,26,…,47,48,49,50).

Um nun die Altersstruktur deiner Stichprobe grafisch aufzubereiten, bietet sich ein Kreisdiagramm an. Aber da gibt es ein kleines Problem. Stell dir mal ein Kreisdiagramm mit 30 Einteilungen (oder „Kuchenstücken“) vor. Nur zum besseren Verständnis habe ich dir die Daten mal in einem Kreisdiagramm aufbereitet (bitte NICHT nachmachen).

Puuuh, irgendwie haben wir es hier nicht geschafft, die Übersichtlichkeit zu verbessern, obwohl das eigentlich das Ziel einer grafischen Darstellung sein sollte. Das bedeutet, dass bei umfangreichen Datensätzen mit vielen verschiedenen Antworten eine Zusammenfassung der Daten erforderlich sein kann.

Fassen wir jetzt das Alter unserer Probanden in Kategorien zusammen:

20-29, 30-39, über 40

Jetzt sieht das ganze doch schon auf den ersten Blick viel übersichtlicher aus. Die erste Abbildung für deinen Ergebnisteil hast du also schon mal. Ein Nachteil beim Zusammenfassen von Daten ist jedoch, dass auf diese Weise Information verloren gehen können.

Bei der deskriptiven Statistik musst du also manchmal zwischen Übersichtlichkeit und Detailgrad abwägen.

Andere häufig gewählte Darstellungsformen sind das Säulendiagramm (auch Histogramm genannt) oder ein sogenannter Boxplot. Wenn du dazu gerne ein separates Tutorial sehen möchtest, schreib einfach einen Kommentar unter diesem Video.

Um solche Diagramme zu erstellen, kannst du neben Excel auch auf spezielle Softwareprogramme wie R oder SPSS zurückgreifen.

Kennzahlen in der deskriptiven Statistik

In der deskriptiven Statistik werden außerdem Kennzahlen verwendet, um einen Datensatz zu beschreiben. Für den Rest des Artikels widmen wir uns deshalb den sogenannten Lageparametern und Streuungsmaßen.

Du verstehst nur Bahnhof?

Keine Sorge, beides ist ziemlich einfach.

Wir schauen uns jetzt an, was es damit auf sich hat. Allerdings können nicht immer alle Kennzahlen für jeden Datensatz gebildet werden, da dies von der Fragestellung und dem Skalenniveau deiner Daten abhängt.

Wenn der Begriff „Skalenniveau“ für dich noch unklar ist, findest du hier ein Tutorial dazu.

Lageparameter

Die Lageparameter dienen dazu, die Tendenz eines Datensatzes zu beschreiben. Sie ermöglichen eine Untersuchung, ob die gemessenen Werte eher groß oder klein sind.

Nehmen wir zum Beispiel eine Umfrage, bei der ermittelt werden soll, ob eher jüngere oder ältere Menschen befragt wurden. Die wichtigsten Parameter, die in diesem Zusammenhang gebildet werden, sind der Mittelwert, der Median und der Modus.

Wir nehmen im Folgenden ein einfaches Beispiel, in dem ein Professor die Daten der Statistikklausur auswertet.

Dazu werden 8 Psychologiestudent:innen gefragt, wie viele Punkte sie in der Statistikklausur bekommen haben.

Proband:in	1	2	3	4	5	6	7	8
Anzahl der Punkte	15	4	20	12	19	12	17	16

Mittelwert (arithmetisches Mittel): Ist der Durchschnittswert deiner Daten. Dieser lässt sich nur berechnen, wenn ein metrisches Skalenniveau gegeben ist.

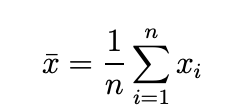
Das heißt für unser Beispiel, dass die durchschnittliche Punktzahl 14,375 Punkte beträgt.

(15+4+20+12+19+12+17+16)/8= 14,375

Modus: Ist der Wert, der in einem Datensatz am häufigsten vorkommt (D). Dieser Parameter kann für alle Skalenniveaus, d.h. auch für Daten mit Nominalskalierung gebildet werden.

D=12

In unserem Beispiel kann man sagen, dass die häufigsten Anzahl an Punkten 12 beträgt, da diese als einziges zwei Mal vorkommt.

Median: Ist der Wert, der genau in der Mitte einer Datenreihe liegt, die nach der Größe geordnet ist. Das heißt also, dass der Median die Datenreihe halbiert, sodass eine Hälfte der Daten unterhalb und die andere Hälfte oberhalb des Medians liegt. Um den Median zu bilden, müssen die Daten ordinalskaliert sein.

1. Schritt: Datenreihe der Größe nach ordnen: 4,12,12,15,16,17,19,20
2. Schritt: Median (Md) berechnen, denn bei einer geraden Anzahl an Daten ist der Median nicht direkt ablesbar.
   Wir nehmen also die beiden Werte, die in der Mitte liegen und teilen diese durch 2.(15+16)/2= 15,5

Md=15,5

Der Median in unserem Beispiel beträgt also 15,5.

Bei ungeraden Datensätzen kannst du den Median direkt ablesen, da dann genau ein Wert in der Mitte liegt.

Streuungsmaße

Oft reichen die Lageparameter aber nicht aus, um die Daten verständlich aufzubereiten.

Deshalb werden in der deskriptiven Statistik ergänzend Streuungsmaße berechnet.

Sie zeigen, wie unterschiedlich die Antworten der Probanden sind und ob es vielleicht Ausreißer gibt. Die deskriptive Statistik arbeitet mit drei standardisierten Streuungsmaßen. Der Varianz, der Standardabweichung und der Spannweite.

In jedem gut sortierten Statistikbuch oder mit einer schnellen Google-Suche findest du die dazu passenden Formeln. Wenn du eine Statistikklausur schreibst, könnte es helfen, die Formeln nachzuvollziehen und zu lernen.

Andernfalls klickst du in deiner Statistik-Software auf „berechnen“ und dann hat sich die Sache.

Hier noch mal unser Beispieldatensatz:

n (Größe des Datensatzes)=8

Maximaler Wert: 20

Minimaler Wert: 4

Varianz: gibt an, wie sich deine Daten um den Mittelwert aller Daten verteilen.

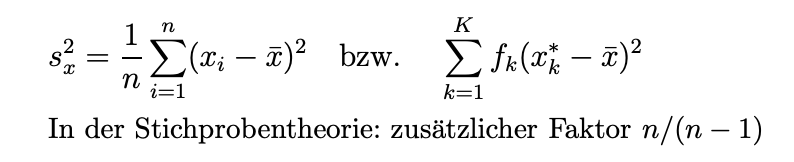
In die entsprechende Formel eingesetzt ergibt sich in unserem Beispiel eine Varianz von 25,98.

Die Varianz ist schwer zu interpretieren, da sie ein Quadrat der Abweichung vom Mittelwert darstellt. Um die Zahl besser nachvollziehen zu können, kannst du daraus die Standardabweichung ermitteln. Jedoch kannst du mithilfe der Varianz, eine weitere Kennzahl berechnen.

Standardabweichung:

Sie gibt an, in welchem Umfang die Daten vom Durchschnittswert abweichen. Der Wert ist die Wurzel der Varianz.

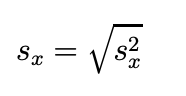
In unserem Beispiel beträgt die Standardabweichung 5,09.

Übertragen auf unser Beispiel beschreibt die Standardabweichung also wie weit die erreichten Punkte im Schnitt von der Durchschnittspunkzahl (aka. Mittelwert) entfernt liegen. Im Schnitt liegen die Werte also plus oder minus 5,09 vom Mittelwert entfernt.

Spannweite: ist der Abstand zwischen dem kleinsten und dem größten Wert des Datensatzes (R).

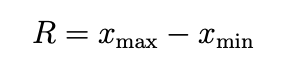
20-4=16

In unserem Beispiel beträgt die Spannweite 16.

Wenn du es bis hierhin geschafft hast, herzlichen Glückwunsch. Die Willenskraft einen Artikel über Statistik bis zum Ende anzuschauen, sagt viel über dich aus.

Jetzt hast du dir in jedem Fall eine Pause verdient, bevor du dich in die Tiefen der deskriptiven Statistik stürzt.

Wenn du auf dem Weg zu mehr Erfolg im Studium noch ein wenig Starthilfe für deine wissenschaftliche Arbeit benötigst, dann habe noch ein PDF für dich, das du dir gratis herunterladen kannst:

Die 30 besten Formulierungen für eine aufsehenerregende Einleitung

---