Was ist ein Histogramm? Wie visualisiert ein Histogramm statistische Daten? Und wie kann dir diese Visualisierung bei der Datenanalyse helfen?

In diesem Artikel zeige ich dir, wie du in der nächsten Statistik-Klausur punkten kannst und mithilfe von Histogrammen deine Datenanalyse auf das nächste Level hebst.

Histogramme sind ein Standardwerkzeug in der Statistik, und wichtig für viele wissenschaftliche Arbeiten. Damit auch du ein Histogramm für solche Zwecke nutzen und verstehen kannst, erkläre ich dir heute dazu die Basics.

Natürlich zeige ich dir auch, wie du ein Histogramm im Handumdrehen für einen beliebigen Datensatz erstellen kannst.

https://youtu.be/BtBGriOdMYk

Was ist ein Histogramm?

Ein Histogramm ist ein Diagramm, das eine Häufigkeitsverteilung darstellt. Wie du in der Grafik siehst, werden auf der x-Achse die Intervalle repräsentiert und auf der y-Achse die entsprechende Häufigkeit.

Charakteristisch für ein Histogramm ist, dass die einzelnen Balken direkt aneinandergrenzen und es keine Lücken dazwischen gibt.

Das liegt daran, dass ein Histogramm für kontinuierliche Daten (z.B. : Messwerte wie Gewicht, Länge oder Zeitspannen) genutzt wird.

Im Gegensatz zu einem Balkendiagramm, das kategoriale Daten (nominale Daten wie z.B. Anzahl der Studenten, die Studienfächer wie Jura, Psychologie, BWL) darstellt. Deswegen werden die Balken bei einem Balkendiagramm getrennt voneinander dargestellt.

Es ist außerdem essenziell, dass die y-Achse eines Histogramms bei der Häufigkeit 0 beginnt. Die Balkenhöhe repräsentiert nämlich die Anzahl der Datenpunkte pro Intervall.

Wenn man nun die Grundlinie verändert, verändert sich die optische Wahrnehmung der Balkenhöhen. Das kann dazu führen, dass die tatsächliche Verteilung der Daten verzerrt wahrgenommen wird. So könnten geringe Datenhäufigkeiten überbewertet oder hohe Häufigkeiten unterschätzt werden.

Wo finden Histogramme Anwendung? Beispielsweise um in der Ökonomie Einkommen innerhalb verschiedener demografischer Gruppen zu analysieren. In der Medizin helfen sie dabei, die Verbreitung von Messwerten wie Blutdruck oder BMI in einer Population zu verstehen.

Aber auch für die Grundlagen der statistischen Datenanalyse sind Histogramme von großer Bedeutung, beispielsweise um einen Datensatz auf Normalverteilung zu prüfen.

Erstellen wir nun ein Histogramm an einem Beispiel

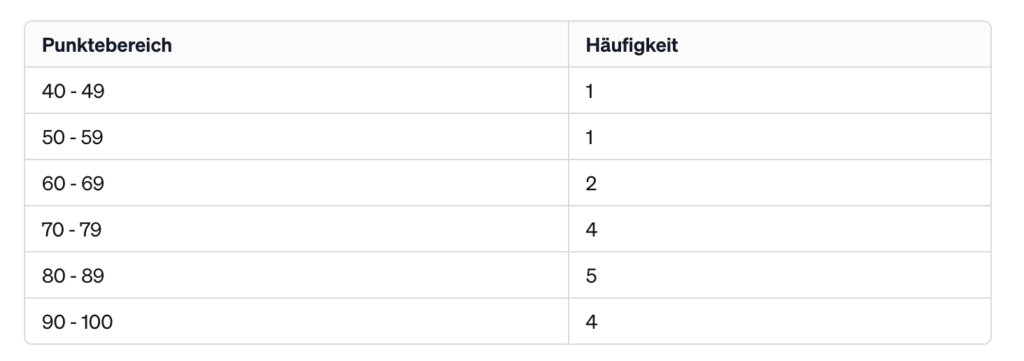
Wir haben eine Datenreihe mit den Punktzahlen aus der letzten Statistikklausur vorliegen:

53, 41, 71, 91, 99, 93, 87, 74, 97, 81, 85, 89, 78, 61, 66, 71, 86.

Zuerst musst du eine Häufigkeitsverteilungstabelle erstellen und die Noten gruppieren.

Die Intervalle müssen zudem die gleiche Breite haben, was wiederum bedeutet, dass die Balken dieselbe Breite haben. Zu breite Intervalle könnten interessante Details verbergen, während zu enge Klassen das Bild zu kompliziert machen könnten. Ich entscheide mich in diesem Beispiel für Intervalle in 10 Punkte Schritten. (40-49, 50-59, 60-69,…).

In der Statistik werden Klassenintervalle für Histogramme oft so gewählt, dass der untere Wert inklusive und der obere Wert exklusive ist.

Das bedeutet, dass ein Intervall von 60-69 alle Werte von 60 bis unter 69 einschließt. Würde man stattdessen ein Intervall von 60-70 wählen, gäbe es eine Unklarheit: Der Wert 70 würde in zwei Intervalle fallen, sowohl in das von 60-70 als auch in das von 70-80. Um diese Doppelzählung zu vermeiden und eine klare, eindeutige Zuordnung von Datenpunkten zu Intervallen zu gewährleisten, überschneiden sich die Intervalle nicht.

Jetzt schauen wir uns die Häufigkeiten an.

Ein Student liegt im Bereich von 40-49. Auch im Bereich 50-59 liegt ein Student. Im Bereich von 60-69 haben wir zwei. 4 Klausurteilnehmer haben zwischen 70 und 79 Punkte erzielt. Und so weiter…

Nun musst die Daten aus der Tabelle mit einem Programm wie Excel oder R in eine Diagrammform bringen. Das Ergebnis sieht für unser Beispiel so aus:

Histogramm verstehen (Interpretation)

Das Interpretieren von Histogrammen ist ein wichtiger Schritt, um deine erhobenen Daten besser zu verstehen. Ein Histogramm zeigt dir visuell, wie die Daten verteilt sind.

Es kann dir helfen, Muster und Anomalien zu erkennen, die auf bestimmte Trends oder Probleme hinweisen. Bitte beachte, dass die Höhe der Balken nicht die Wahrscheinlichkeiten wiedergibt, denn es sind die Flächen der Balken, die dies tun.

1. Datenverteilung

Histogramme stellen die Häufigkeit von Daten in verschiedenen Intervallen dar und helfen, die Verteilung der Daten auf einen Blick zu erfassen. Forscher können leicht erkennen, ob die Daten normalverteilt, links- oder rechtsschief sind oder ob sie andere Verteilungsformen wie bimodale Verteilungen aufweisen.

Eine normalverteilte Form, oft als Glockenkurve bezeichnet, bedeutet, dass die meisten Daten um einen zentralen Wert konzentriert sind, mit symmetrischen Schwänzen zu beiden Seiten. Im universitären Kontext könnte dies die Verteilung der Prüfungsergebnisse sein, bei der die meisten Studierenden Durchschnittsnoten erhalten und nur wenige sehr hohe oder sehr niedrige Noten.

Eine schiefe Verteilung zeigt, dass die Daten asymmetrisch verteilt sind. Ist ein Histogramm nach rechts (positiv) geneigt, gibt es eine Anhäufung von niedrigen Werten mit einigen wenigen hohen Werten, wie es vielleicht bei der Zeit sein könnte, die Studierende für ein bestimmtes Fach aufwenden. Viele verbringen wenig Zeit, aber wenige investieren sehr viel. Eine nach links (negativ) geneigte Verteilung deutet auf das Gegenteil hin.

Eine bimodale Verteilung mit zwei Spitzen könnte auf das Vorhandensein von zwei unterschiedlichen Gruppen hinweisen. Betrachten wir zum Beispiel die Notenverteilung in einer Vorlesung, die sowohl von Erstsemestern als auch von fortgeschrittenen Studierenden besucht wird. Zwei Spitzen könnten darauf hinweisen, dass beide Gruppen tendenziell unterschiedliche Ergebnisse erzielen.

2. Auffälligkeiten erkennen

Durch die Visualisierung können Ausreißer, ungewöhnliche Muster oder Anomalien in den Daten erkannt werden, die weitere Untersuchungen erfordern könnten. Die Breite der Daten zeigt z.B. an, wie die Daten gruppiert sind.

Schmale Balken können auf eine detaillierte Datenverteilung hinweisen, während breitere Balken eine allgemeinere Übersicht bieten. Die Höhe der Balken zeigt die Häufigkeit oder Anzahl von Beobachtungen in jedem Intervall. Höhere Balken bedeuten eine größere Anzahl von Beobachtungen in diesem Bereich.

3. Vergleich von Datensätzen

Histogramme ermöglichen auch den Vergleich von zwei oder mehreren Datensätzen. Du kannst sie nutzen, um zu sehen, wie sich die Daten unter verschiedenen Bedingungen oder über verschiedene Gruppen verteilen.

4. Hypothesen testen

Histogramme können bei der Formulierung oder Überprüfung von Hypothesen über die Daten hilfreich sein. Beispielsweise könnte deine Hypothese sein, dass eine bestimmte Variable normalverteilt ist, was durch ein Histogramm bestätigt oder widerlegt werden kann.

5. Entscheidungsfindung

In der Praxis, beispielsweise in der Qualitätssicherung, kann ein Histogramm verwendet werden, um zu bestimmen, ob ein Geschäftsprozess bestimmte Spezifikationen erfüllt.

Interpretation des Beispiel-Histogramms

Um ein besseres Gefühl für Histogramme zu bekommen, stelle ich dir im Folgenden ein paar Fragen zu unserem Beispielhistogramm. Pausiere gern nach jeder Frage und versuche die Aufgabe allein zu lösen, bevor du die Lösung abspielst.

Würdest du sagen, dass die Daten symmetrisch sind? Oder würdest du sagen, dass sie nach rechts oder links geneigt sind?

Du siehst, dass wir höhere Balken auf der linken Seite haben. Daher könnten wir sagen, dass diese Art von Daten nach links geneigt sind, oder anders gesagt, sie haben eine negative Schiefe. Sie sind nicht nach rechts geneigt und nicht symmetrisch. Die Studenten haben in dieser Klausur also eher höhere Punktzahlen erreicht.

Was ist der Modus für diese speziellen Daten? Der Modus ist im Grunde der Bereich, der in diesem Fall die höchste Häufigkeit aufweist. Die meisten Schüler erhalten zwischen 80 und 89 Punkten. Dieser Bereich wäre dann der Modus für unser beispielhaftes Histogramm.

Wie viele Studenten haben bis zu 69 Punkte in der Klausur?

In diesem Fall musst du die ersten 3 Balken addieren.

1+1+2= 4

4 Studenten haben bis zu 69 Punkte erzählt.

Wie viele Studenten haben mindestens 80 Punkte erhalten?

In diesem Fall musst du die letzten 2 Balken addieren.

5+4= 9

9 Studenten haben mindestens 80 Punkte erzählt.

Wie viele Studenten haben zwischen 60 und 89 Punkte erzielt?

In diesem Fall musst du die mittleren Balken addieren.

2+4=5= 11

11 Studenten haben zwischen 60 und 89 Punkte erzielt.

Histogramme und Wahrscheinlichkeiten

Mit Histogrammen kannst du dich besser durch große Datenmengen navigieren. Die grafischen Darstellungen bilden Wahrscheinlichkeitsverteilungen ab, die entscheidend sind, um die Dynamik in einem Datensatz besser zu verstehen.

Nehmen wir wieder unser Beispiel der Prüfungsergebnisse einer Klausur. An der Höhe der Balken im Histogramm kannst du ablesen, wie viele Studenten in bestimmte Notenspannen fallen.

Doch diese Balken sind mehr als nur Zahlenintervalle. Denn sie zeigen auch die Wahrscheinlichkeit, mit der ein zufällig ausgewählter Student ein bestimmtes Ergebnis erreichen könnte.

Eine Gruppierung der Ergebnisse um einen zentralen Wert deutet auf eine Normalverteilung hin. Viele statistische Tests gehen von einer Normalverteilung der Daten aus. Das Histogramm zeigt uns, ob diese Annahme zutrifft oder du vielleicht einen anderen Testansatz wählen solltest.

Histogramme können dir auch helfen, Schlüsse über eine Gesamtpopulation aufgrund einer Stichprobe zu ziehen. So kann das Histogramm einer Klausur uns Aufschluss über das Abschneiden aller Studierenden eines gesamten Studiengangs geben.

Alles in allem ist das Histogramm also ein Schweizer Taschenmesser im Werkzeugkoffer jeder Statistikexpertin. Wenn du jetzt noch etwas tiefer in das Thema einsteigen möchtest, empfehle ich dir einen Blick in das Buch „Discovering Statistics“ von Andy Field.